Motion Data Outputs
You can export the downloaded measurement by selecting it in the Library tab. Swipe left on the desired measurement, you will see the Export button. The CSV can then be shared using the standard share methods of your phone/tablet. On Android, you can also get the exported files in /SDCard/notch_library folder.
Available data outputs:
- Joint angles
- Positions
- Local Sensor Acceleration
- Local Sensor Gyroscope
- Global Sensor Acceleration
- Global Sensor Gyroscope
- Quaternions This feature is only available through our SDK
Example
We created a 1 notch measurement on a theoretical chest. You can check the measurement here.
You can download its generated export data from here.
Coordinate system
The coordinate system in which the quantities (quaternions, vectors, etc.) are defined is fixed to our visualiser’s 3D frame: Y-up, X-left, Z-forward.
Acceleration / Gyroscope
Gravity is removed from the acceleration data, so it’s 0,0,0 when the body part is not moving at all.
Gyroscope 0,0,0 means it’s not rotating at all. Units are in SI (m/s^2 and 1/s).
Joint Angles
Exported File Name: angles_{bone_name}.csv
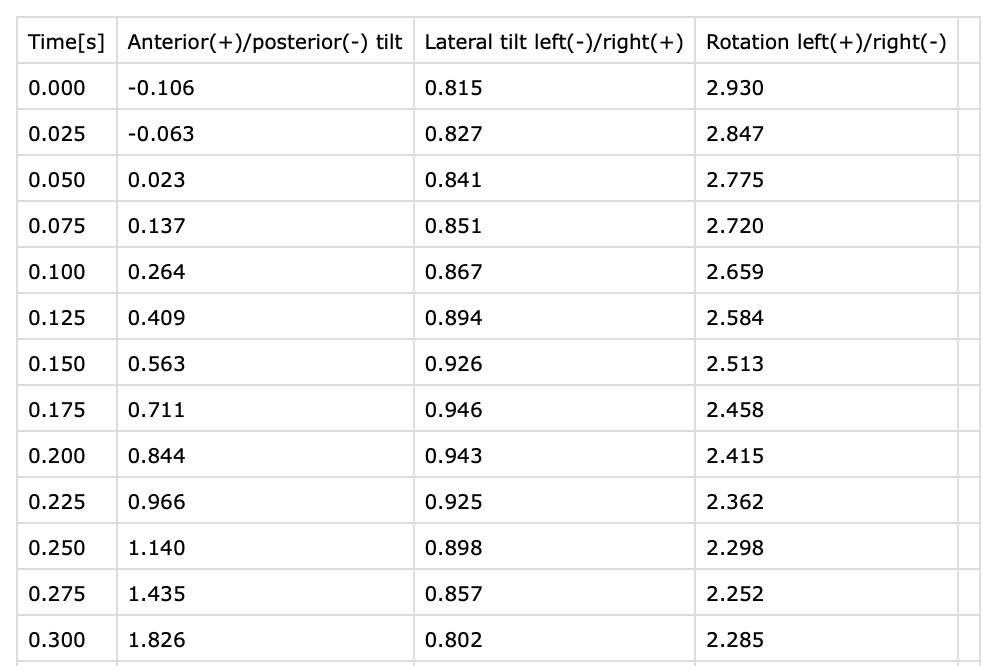
You can obtain the joint angles by downloading the .CSV files from the Web Library or by exporting and sharing directly from the Notch Pioneer App. The joint angle data is the angular distance between the user’s bone orientation and the initial steady orientation, in the given time frame, measured in degrees, segmented as:
- anterior / posterior tilt,
- lateral tilt,
- rotation.
Some joints have fewer degrees of freedom. In the example above, the user’s chest remained in close to uan pright position for the first 0.3sec.
Good to know Joint angles are relative distances between two bones. For example, the RightKnee is the angle between the RightThigh and the RightLowerLeg. The angle of a particular bone (e.g. RightLowerLeg_bone.csv) is the angle measured from the steady measurement’s orientation, which is not the global up.
Positions
Exported File Name: positions_{bone_name}.csv
Lateral Movement
Lateral movement is the distance traveled by the skeleton. Lateral movement is calculated by knowing the orientation of the legs, hips, and the length of the bones. To access the lateral movement data, look for the Pos_z (forward) in the position_bone.csv, we recommend you look at the data of the Root or the Hip.
Important Only non-real-time recordings with Lower Body Configuration (including Hip, Thighs and LowerLeg) generate lateral movement data.
Local Sensor Acceleration / Gyroscope
Requires Extended License
Local sensor vector origin is defined when the original skeleton has been created.
This variant transforms this data into the bone’s local coordinate system (i.e. transforms it with its actual orientation). These are strictly sensor data, so the accelerometer data depends on the position of the notch on the body part. Gyro data, however, is independent as long as the body part is considered to be rigid.
Global Sensor Acceleration / Gyroscope
Requires Extended License
Global sensor vector origin is referencing the steady measurement’s orientation.
Quaternions
For visualization, we use quaternions and we derive the biomechanical angles (which are shown in the visualizer and are exported to csv) from them. These angles are not pure Euler angles - we modified them to suit or purposes and to match the conventions used in biomechanics/healthcare - but are related to them. Read more info on quaternions
To access the quaternion data, you need to deploy your own custom application.
Once you set up your project, you can get the quaternions from your VisualiserData object. This provides the bone’s orientation represented by the quaternion q=[cos(a/2),ux,uy,uz], where u=[ux,uy,uz] is the (normalized) axis of the rotation and a is the angle of the rotation. This is our basic quaternion definition.
All rotations are absolute, not relative to the previous bone in the chain.
getQ: quaternion (orientation) of a bone. (w,x,y,z) = (cos(t/2), uxsin(t/2), uysin(t/2),uz*sin(t/2)), which represents a rotation around axis u=(ux,uy,uz) with angle ‘t’ (in radians).
If you prefer to work with rotation matrices instead of quaternions, you can transform them with quaternion.getRMX(). Or if you prefer Euler angles, you can calculate them either from the quaternion, or the rotation matrix, but these are not implemented in our system due to various types/definitions of Euler angles.
Gimbal Effect Please note, quaternions (as Euler angles) are affected by the gimbal lock effect. The main problem is quite simple: in some special directions one (ore more) of the angles becomes undefined, or not uniquely defined. You will need to consider this when using quaternions to motion analysis.
Work-around If you do not want to develop your own application, you can also export the recordings to bvh format, which is a common motion capture format. There are plenty of editor apps which can handle bvh files, and some of those can even export to quaternions and Euler angles, since the bvh files are also based on Euler angles.